4.1     Conformal Approximation for Irregular Geometries

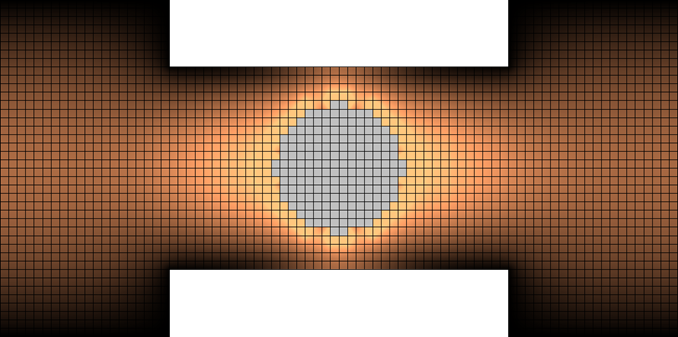
Classically, in FDTD method the analysed circuit is divided into cuboidal cells, where each cell composes of only one medium. This type of meshing (dividing into cells) is called stair-case and is shown in Stair-case FDTD meshing example picture. Classical FDTD stair-case meshing radically corrupts the physical geometry. Good shape imitation can be approximated by mesh refinement, but it should be noted that it drastically increases memory occupancy and simulation time, e.g. decreasing the cell size in all three directions by 2, increases the memory occupation by a factor of 8, and the computing time 16 (!) times. There are various conformal FDTD techniques for better approximation of curved shapes, but they usually require time-step reduction (proportional to the smallest cell maintained) and hence longer simulation time. QuickWave uses original, advanced, and unique conformal FDTD formulation developed by the authors of the software. The FDTD method has been enhanced with conformal boundary models, which allow precise and accurate modelling of curved shapes and obtaining high accuracy simulation results without time-step reduction. The result of conformal FDTD meshing is shown in Conformal FDTD meshing in QuickWave picture. An improvement over classical FDTD is immediately visible. Let us emphasise that in both cases we are talking about an actual internal representation of the 3D geometry in the electromagnetic simulation process, and not about the graphical display shown by the geometry editor.

Stair-case FDTD meshing example.

Conformal FDTD meshing in QuickWave.