1.2 Plane wave at the media boundary
In previous paragraph, a plane wave propagation in homogeneous, linear and isotropic medium has been discussed. In this paragraph a plane wave incident at the two homogeneous media boundary will be considered. The model used in this paragraph is named ppw5.QWpro. It is assumed that the wave incidents normally at the media boundary.
Fig. 13 shows a situation in which a plane wave incidents at the media boundary. In this case 3 types of waves can be described:
· incident wave, ![]() ,
, ![]() ,
,
· reflected wave, ![]() ,
, ![]() ,
,
· transmitted wave, ![]() ,
, ![]()

Fig 13 Graphic scheme of normal wave incidence at two mediums border.
In this case a reflection coefficient, describing a reflected to an incident field ratio, can be defined:
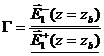
This allows determining the formulas describing the waves defined above:
Incident wave:
![]()
![]()
Reflected wave:
![]()
![]()
Transmitted wave:
![]()
![]()
The reflection coefficient G can be calculated due to the assumption that impedance at the media boundary must be continuous:
![]()
The above wave formulas confirm that in medium 1 incident and reflected waves merge, giving partially standing wave, as constant maxima and minima of fields’ envelopes distribution in space exists (a standing wave property) and also the energy is transferred in a direction of an incident wave propagation (typical for traveling wave). In case of medium 2, only traveling wave exists.
The predominant wave type in medium 1 can be determined using the standing wave ratio SWR (or VSWR) defined as the ratio of maximum field envelope (electric or magnetic) to minimum field envelope:

SWR is related to a reflection coefficient according to the following formula:
![]()
Please note that the value of SWR varies in the range (1; ∞). If SWR tends to 1, we deal with a more traveling-like wave.
The objectives of this paragraph are: