4.5.1 Introduction
QuickWave software enables consideration of heat transmission between two planes, which are not in contact with each other. The energy flow is due to the temperature difference between any pair of points (cells) on the separated planes.
The simpliest formula, describing emitted radiative power can be written for a perfectly black body with a fully convex surface and uniform temperature:
where: σ = 5.670374419...×10−8 W⋅m−2⋅K-4 stands for Stefan-Boltzmann constant, A is surface (in m2), and T is surface temperature (in Kelvin). The radiative power J includes entire energy radiated (at each wavelength and angle). The formula includes only the radiation emitted due to the temperature of the body.
In real world black bodies do not exist and the real radiative power is smaller than that given with formula (1), and therefore, an emissivity factor ε (where 0≤ε≤1) has to be included:
The formula (2) describes a perfectly gray body. The factor ε might be assigned to the color of the surface – the darker the color, the greater radiation power. For a perfectly white surface the factor ε is equal zero. Moreover, in case of a light incident on a surface, the factor ε is equal to the percentage of the radiation absorbed and the factor 1-ε is the percentage of the radiation reflected (reflection factor).
For real applications at least two surfaces with different temperatures have to be considered. The most simple formula for a ”netto” flow can be written in case of two parallel, infinite, perfectly black walls:
where T1 and T2 are uniform temperatures of the surfaces. It is desired to extend the formula to the case of two walls with different emissivity factors, ε1 and ε2 respectively. By studying multiple beam reflections between the surfaces, the following generalized formula can be written for two parallel, infinite perfectly gray surfaces:
The denominator of the multiplication factor on the right side is a sum of a geometrical series, which represents the intensities of the multiply reflected beam.
Next, it is desired to study a pair of surfaces separated by an arbitrary distance and with arbitrary orientations. Owing to the fact that the radiation intensity towards different angles is proportional to cos θ, where θ is the angle between the considered direction and the vector normal to the surface, one can write a general formula for a ”netto” radiation power between two arbitrarily oriented, perfectly black bodies (from body 1 to body 2):
where A1 and A2 are the surfaces of the bodies, and F1→2 is a view factor, which is defined as an integral:
where 
and 
are infinitesimal parts of both surfaces, and 
and 
are the angles between the line between those infinitesimal parts and their normal vectors respectively. The distance between those infinitesimals is s. It is worth noting that the formula (5) does only describe the part of radiation emitted from body 1, which incides onto the body 2. It does not include the radiation emitted in other directions. In real world, both the bodies would be surrounded by another enclosure with its temperature distribution and non-negative reflection coefficients. If the temperature of the enclosure is positive (greater than 0 K), then it emits the radiation, which is further absorbed by body 1 and body 2. Moreover, if the reflection coefficient of the enclosure is positive, then the radiation emitted by body 1 reflects from the enclosure and incides onto body 2.
Finally, we intend to write down an analogous formula for the case of two arbitrarily oriented perfectly grey bodies. This case, however, is much more complicated, because multiple reflections between each surface (and the enclosure) have to be considered. In QuickWave we consider only a simplified case of the bodies, which emit the radiation only in directions from one body to another, while the radiation emitted in other directions (towards a hypothetical enclosure – surrounding), is reflected back immediately towards the emitting body. In this simplified case, the ”netto” flow takes a form:
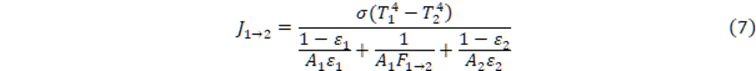
The formula (7) is the base of the implementation made in QuickWave, which is explained in the next Implementation in QuickWave chapter.