Field Integration Along Contours
Area of applications of QuickWave software for electromagnetic design and simulations.
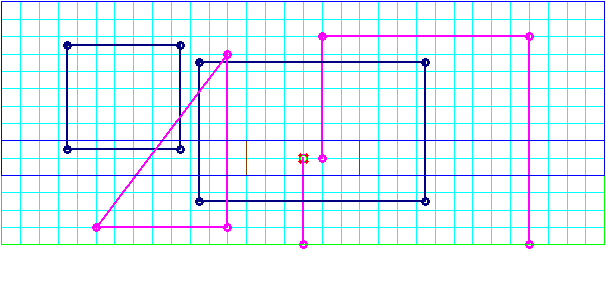
Currents and voltages extraction by integrating H-fields along a virtual loop surrounding a conductor and E-fields along a virtual line connecting two conductors.
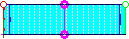
Path of integration in the parallel-plate transmission line.
Contours E, H and combination of them.
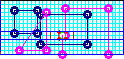
Fields along user-defined contours - impedance and power extraction (V2D BOR).