
6.2.9 Radiation and Scattering
The radiation and scattering calculations deliver the following data:
QuickWave allows calculating radiation patterns of radiating structures using the Near to Far (NTF) post-processing. For radiation pattern calculation the so-called Huygens surface is required. This is the surface of the near-to-far field transformation, called in brief NTF Box, whereat the tangential near fields directly produced by the FDTD simulation are transformed into the far field radiation patterns using Green’s function.
NTF post-processing performs the near-to-far field transformation in the frequency domain to calculate the radiation patterns of a radiating structure, at frequencies specified by the user. The results are available in the Results window for 2D radiation pattern results. The characteristics available in QW-3D are absolute values and phases of the theta- and phi-polarisation at NTF frequencies, set in the Input Interface. In QW-V2D co-polar and cross-polar patterns are additionally calculated following Ludwig's third definition.
The NTF post-processing is available only if NTF box has been previously defined in the Input Interface. The NTF frequencies can be introduced in the Input Interface in any order and theoretically any number of them can be considered. However, note that collecting the NTF data for each new frequency (Fourier transforms of four field components in each cell on the NTF box) is quite consuming in terms of computer memory and computing time.
Remember that for correct radiation pattern extraction, the NTF box must fully surround the structure and be itself surrounded by a homogeneous medium terminated with absorbing boundaries (except for symmetry and ground planes). A majority of Near to Far applications are in air, which is a natural environment for a majority of antennas. However, radiation patterns and antenna efficiency in dielectrics, and even in lossy dielectrics, may be of interest in e.g. biomedical studies. Near to Far post-processing in QW-3D has been especially adapted to such cases; for more detail please refer to Radiation pattern in an arbitrary isotropic medium.
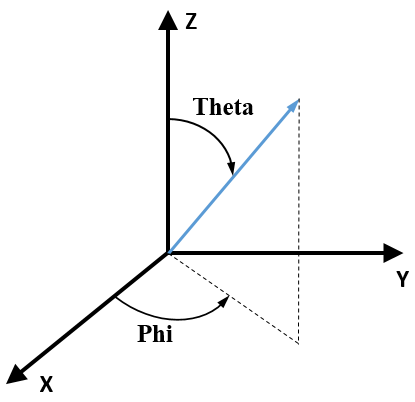
In QW-Simulator, the far fields are available for any directions in space, with Reference Axis, Reference Point, angles and gain scaling options set in QW-Simulator. The far field patterns are calculated in a spherical coordinate system with one Reference Axis and two angles: elevation (Theta) and azimuthal (Phi). The picture below (for user’s convenience presented also in Radiation Patterns dialogue) shows the sense of Theta and Phi when the Reference Axis is Z. If another Cartesian axis (X or Y) is chosen as the Reference Axis the below picture will change accordingly.
In QW-V2D the only available reference axis is X (the axis of rotation).

A rare feature of QW-3D resides in allowing a so-called arbitrary Reference Axis - Axis Z', of any orientation in space. It is done by defining the Euler Angles. Precisely speaking, the original XYZ coordinate system will be transformed as follows:
first, it is translated so that the origin is located at Reference Point,
then it is rotated using defined Euler Angles.
The position of the Reference Point does not influence the absolute values of the far field radiation patterns (in lossless NTF background medium) but it does influence their phase characteristics. A possibility of modification of the Reference Point coordinates facilitates searching for a phase centre of the antenna. The Reference Point position is expressed in the same coordinates and units as those used in the project and defined in the Input Interface.
As regards the meaning of the Euler Angles, several conventions can be found in the literature, and the following one has been adopted in QuickWave software:
First the coordinate system is rotated clockwise from X axis around the original Z-axis, by Precession angle Alfa (0 £ Alfa £ 360). This keeps the Z-axis unchanged while the X- and Y-axes are rotated in the XY-plane, becoming intermediate axes Xint and Yint.
Then the intermediate coordinate system is rotated clockwise around the intermediate Yint-axis, by Nutation angle Beta (0 £ Beta £ 180). This keeps the intermediate Yint axis unchanged while the original Z and intermediate Xint axis are rotated in the XintZ-plane. This produces the new Z' axis and the second-intermediate Xint2.
Finally the second intermediate coordinate system is rotated clockwise around the new Z'-axis, by Rotation angle Gamma (0 £ Gamma £ 360). This produces the new X' and Y' axes.
For the avoidance of doubt, the versors of the new axes X', Y' and Z' in the old XYZ coordinates are calculated by the software and displayed in the lower right part of the Radiation Patterns dialogue.
The radiation pattern will be calculated in the new X'Y'Z' coordinate system, with reference axis Z', and Phi angle calculated from X' axis clockwise.
QuickWave allows choosing between radiation patterns calculated:
with respect to Theta angle (with constant Phi, for Theta step, starting value and end value set by the user),
with respect to Phi angle (with constant Theta, for Phi step, starting value and end value set by the user).
QuickWave offers following gain scaling options: directive gain, power gain, absolute_1port gain, absolute gain and Fields at 1m, as described in Antenna Gain.
Finally, it is worth noting that if there are one, two, or three electric or magnetic walls detected at any of the NTF walls, QW-Simulator will then perform NTF calculations with Green's functions appropriate for the resulting half- quarter- or one-eights of space. However, note that there is ambiguity in gain calculations between two scenarios such as: one dipole radiation over a physical ground plane or a system of two dipoles in free space, a half of which is simulated with a symmetry plane. These two scenarios are identically defined from the viewpoint of the simulated geometry but physically they differ by 3 dB in gain and efficiency values. The second case (free space with symmetry planes) is default in the software, however, the user may direct the software and set the number of physical ground planes present in the scenario for correct gain and efficiency values calculation. This is available through Number of ground planes option in Radiation Patterns dialogue. For practical discussion refer to User Guide 3D: One dipole near electric wall.
At the end of this section let us point out some useful information concerning placing the NTF and absorbing boxes for the purpose of getting accurate NTF post-processing results:
NTF surface can be relatively close to the radiating object. Two-three cells of separation are usually sufficient in the case of antennas fed by transmission lines. A bigger distance may be required in the case of dipoles radiating in free space since they can generate quasi-static mode around them and perturb the correct calculation of radiated power with Radiated Power calculated from NTF fields option.
The separation between NTF surface and absorbing boundary must not be smaller than three FDTD cells. Otherwise the far field calculation may be incorrect. Note that QW-Editor displays full cells in XY plane but half-cells in XZ or YZ planes. Thus when watching the QW-Editor displays in XZ or YZ we need to make sure that a distance of at least six half-cells is maintained.
QuickWave allows calculating far field scattering patterns of scattering structures irradiated by a plane wave, using the Near to Far (NTF) post-processing. For scattering pattern calculation the so-called Huygens surface is required. This is the surface of the near-to-far field transformation (called in brief NTF box), whereat the tangential near fields directly produced by the FDTD simulation are transformed into the far field scattering patterns using Green’s function.
NTF post-processing performs the near-to-far field transformation in the frequency domain to calculate the scattering patterns of a scatterer, at frequencies specified by the user. The results are available in the Results window for 2D radiation pattern results. The characteristics available in QW-3D are absolute values and phases of the theta- and phi-polarisation at NTF frequencies, set in the Input Interface.
The NTF post-processing is available only if NTF box has been previously defined in the Input Interface. The NTF frequencies can be introduced in the Input Interface in any order and theoretically any number of them can be considered. However, note that collecting the NTF data for each new frequency (Fourier transforms of four field components in each cell on the NTF box) is quite consuming in terms of computer memory and computing time.
Remember that for correct scattering pattern extraction, the NTF box must fully surround the structure and be itself surrounded by a homogeneous medium terminated with absorbing boundaries. A majority of Near-to-Far applications are in air, which is a natural environment for a majority of scattering problems. However, scattering patterns in dielectrics, and even in lossy dielectrics, may be of interest. Near to Far post-processing in QW-3D has been especially adapted to such cases; for more detail please refer to Radiation pattern in an arbitrary isotropic medium.
In QW-Simulator, the far fields are available for any directions in space, with Reference Axis, Reference Point, angles and gain scaling options set in QW-Simulator. The far field scattering patterns are calculated in a spherical coordinate system with one Reference Axis and two angles: elevation (Theta) and azimuthal (Phi). The picture below (for user’s convenience present also in Radiation Patterns dialogue) shows the sense of Theta and Phi when the Reference Axis is Z. If another Cartesian axis (X or Y) is chosen as the Reference Axis, the below picture will change accordingly.

A rare feature of QW-3D resides in allowing a so-called arbitrary Reference Axis - Axis Z', of any orientation in space. It is done by defining the Euler Angles. Precisely speaking, the original XYZ coordinate system will be transformed as follows:
first, it is translated so that the origin is located at Reference Point,
then it is rotated using defined Euler Angles.
The position of the Reference Point does not influence the absolute values of the far field scattering patterns (in lossless NTF background medium) but it does influence their phase characteristics. The Reference Point position is expressed in the same coordinates and units as those used in the project and defined in the Input Interface.
As regards the meaning of the Euler Angles, several conventions can be found in the literature, and the following one has been adopted in QuickWave software:

First the coordinate system is rotated clockwise from X axis around the original Z-axis, by Precession angle Alfa (0 £ Alfa £ 360). This keeps the Z-axis unchanged while the X- and Y-axes are rotated in the XY-plane, becoming intermediate axes Xint and Yint.
Then the intermediate coordinate system is rotated clockwise around the intermediate Yint-axis, by Nutation angle Beta (0 £ Beta £ 180). This keeps the intermediate Yint axis unchanged while the original Z and intermediate Xint axis are rotated in the XintZ-plane. This produces the new Z' axis and the second-intermediate Xint2.
Finally the second intermediate coordinate system is rotated clockwise around the new Z'-axis, by Rotation angle Gamma (0 £ Gamma £ 360). This produces the new X' and Y' axes.
For the avoidance of doubt, the versors of the new axes X', Y' and Z' in the old XYZ coordinates are calculated by the software and displayed in the lower right part of the Radiation Patterns dialogue.
The scattering pattern will be calculated in the new X'Y'Z' coordinate system, with reference axis Z', and Phi angle calculated from X' axis clockwise.
QuickWave allows choosing between scattering patterns calculated:
with respect to Theta angle (with constant Phi, for Theta step, starting value and end value set by the user),
with respect to Phi angle (with constant Theta, for Phi step, starting value and end value set by the user).
QuickWave offers following gain scaling options: directive gain, power gain, absolute_1port gain, absolute gain and Fields at 1m, as described in Antenna Gain.
It is worth noting at this point that QuickWave enables calculation of the scattering patterns of periodic structures, analysed using periodic boundary conditions. For this kind of problems the software automatically calculates the directions of higher diffraction order beams following the relation:
![]() ,
,
where q inc is an illumination angle, qm is the mth (m³0) diffraction order and L stands for the spatial period of the structure. The illumination and reflection (of higher orders) angles are indicated in the scattering pattern with the vertical dashed lines. Note that due to the finite size of NTF wall, where the Fourier transform is performed, the scattering pattern maybe somewhat broadened, rather than the Dirac delta. Nevertheless, nulls of the broadened incident beam are located within the numerical accuracy at all of the diffraction orders. In general, it may be proven that if NTF is processed over the integer multiple of spatial periods of the structure, all the scattered beams do not disturb one another in the scattering pattern. This is advantageous because we can use NTF in a periodic scenario that is often electrically short and easily extract the reflection coefficient for any diffraction order.
The discussion on higher diffraction orders is given for User Guide 3D: Plane wave excitation example.
6.2.9.3 Radiation pattern at chosen Huygens surface
The NTF box consists of six Huygens surfaces, where the near field to far field transformation is performed. The principle of near-to-far field transformation requires the radiating structure to be surrounded by a closed surface, unless symmetries are explored. This is the approach taken in the antenna scenarios: for a majority, NTF surface has been a closed cuboidal box. There are, however, cases when we may wish to calculate radiation patterns using only some of the NTF pickup walls. A practical application would be to directly compare simulated and measured results, with near-field measurements taken over a single aperture. Another case is more FDTD-specific: due to numerical dispersion and the necessity to average either electric or magnetic field components across each pickup wall, a wave that physically propagates in one direction may numerically generate a non-physical backward lobe (see [176]). A simple way to see whether a particular backward lobe is physical or a numerical artefact, is to disconnect the pickup surface "looking" in its direction from NTF transform and to check how the results change. QuickWave enables such functionality and allows excluding selected NTF walls from the near-to-far field transformation. This feature is available in the Radiation Patterns dialogue as NTF Walls option. In QW-3D, by default, all six walls are checked and take part in the NTF transformation. The user may uncheck and exclude any combination of them from one NTF processing. Note that in QW‑V2D, three walls are automatically excluded from choice in the dialogue.
Using the above described option may be followed through on User Guide 3D: Disconnecting NTF walls example.
6.2.9.4 Radiation pattern in an arbitrary isotropic medium
The near-to-far field transformation is usually applied in air, being the most typical environment for antennas. However, there are cases when transforming near fields to far fields in homogeneous media other than air or even lossy dielectrics is of interest. These may be biomedical applications or other cases of microwave propagation in large bodies. The air-formulation of NTF cannot be applied because impedance relation between the electric and magnetic field becomes different, and so does the propagation constant used in distance normalisation. NTF post-processing in QuickWave has been extended in response to such needs.
Summarising, the region in which the radiating object (and thus the NTF box) is placed must be homogeneous but may be filled with a medium of arbitrary permittivity εr, permeability μr, conductivity sigma and magnetic loss sigmaM. However, NTF post-processing will not automatically recognise the medium parameters and thus the user should put attention to two things while setting up the simulation scenario in the Input Interface:
- the effective permittivity of all absorbing boundaries of Mur ABC type should be set to:
Permittivity (effective) = εrμr;
for PML boundaries the software automatically adjusts PML parameters to the surrounding medium;
- the user should instruct NTF post-processing to follow the non-air procedures; this is done by setting explicitly the required medium parameters for the NTF background medium in the Input Interface or via a UDO object named ntfbkg.udo and available in the ..elib/actions library.
It should be noted at this point that if NTF background medium is set as lossy, the full set of gain scaling options is available only if radiated power is calculated from the 3D patterns in the far zone. Power integration over the NTF box gives a result dependent on the box position and shape, and cannot be used as a reference for scaling the radiated fields. Thus only unscaled values of Fields at 1 m are available in such a case.
The discussion about how a special variant of NTF post-processing is indeed needed to obtain physically correct results is given in User Guide 3D: Near-to-Far field transformation in non-air and lossy regions.
QuickWave offers several scaling options for the antenna gain, which are available as Gain Reference option:
Directive – it refers to directive gain calculated with respect to the power radiated by the antenna. It is given as a unitless value.
In this case the result denoted by |Epol| (where pol denotes polarisation of the considered radiated wave and may be equal theta, phi, left or right) has the following sense, when presented in the quadratic scale:
|Epol|(theta, phi) = 4π Kpol(theta, phi) / Pr.
In linear scale, a square root of the above quantity is displayed. Above, Kpol is the radiation intensity of the considered polarisation pol in the considered direction (theta, phi), that is, the power radiated in this direction per unit solid angle. Kpol can also be understood as the magnitude of the radially directed Poynting vector multiplied by the square of the distance r from the reference point:
Kpol(theta, phi)=r2 |Epol(r, theta, phi) x Hpol(r, theta, phi)|
where Epol(r, theta, phi) and Hpol(r, theta, phi) are the electric and magnetic field vectors of the considered polarisation at the far zone point (r, theta, phi).The argument denoted by <Epol is the phase of the electric field (which, in the case of lossless NTF background medium, is also the phase of the magnetic field).
It means that power density radiated in a particular direction is divided by radiated power density of isotropic antenna, radiating the same total power Pr. Thus the software needs to calculate the total power radiated by the antenna as a reference value. There are two methods of doing this available in QW-3D that are described in Radiated Power.
Power – it equals to Directive gain multiplied by radiation efficiency in quadratic scale (i.e., in linear scale, Power gain equals to Directive gain multiplied by a square root of antenna efficiency). Remember that efficiency is not available (Ef=0) if S‑Parameters post-processing is not activated or NTF frequency is not one of S‑Parameters frequencies.
Absolute_1port - (called Absolute up to version 7.5) it equals to Power gain multiplied by the coefficient of reflection loss (1-|S11|2) in quadratic scale (i.e., a square root of this coefficient in linear scale). In typical antenna problems with a single port (N=1 in S-Parameters), Absolute_1port gain equals to Absolute gain (subject to numerical errors and provided that data for both types of gain are available).
Absolute – it is calculated similarly to the Directive gain with this difference that here the power available from the source is taken as a reference. Its calculations require that Power Available post-processing be available, with the considered NTF frequency being one of Power Available frequencies.
Relative – it is calculated through normalisation to the highest value of the displayed pattern (except for cross-polarisation patterns normalised to the highest values of the corresponding co-polarisation patterns).
Fields at 1m – it refers to the absolute value of the field intensity generated by the antenna in the far zone under the considered conditions (with the level of radiated power as displayed in the 2D radiation pattern Results window). The 1m distance has been chosen here arbitrarily, assuming that 1m will indeed be in the far zone for microwave antennas. Rigorously, we should say that this option gives radiated field in the far zone, scaled to 1m distance from the reference point using exp(-α*r)/r far field dependence (where r is distance from the reference point and α is attenuation constant in the NTF background medium). The considered field is electric field in [V/m] divided by square root of intrinsic impedance in [Ω] of NTF background medium (which is typically air, unless set otherwise by the user when configuring the NTF box or NTF post-processing in the Input Interface). Equivalently, this is magnetic field in [A/m] multiplied by square root of NTF background medium impedance in [Ω], or square root of radiated power density (square root of Poynting vector) in [W/m2]. Note that in lossless media, values scaled to 1m distance and expressed in "unit per m" are equal to values scaled to 1mm distance and expressed in "unit per mm", which are the units used for EM fields in other co- and post-processings of QW-Simulator.
RCS – it refers to the Fields at 1m scaled by Power Available from the Plane Wave source.
QuickWave calculates the total power radiated (Pr) from the antenna at given NTF frequencies. It is a time-maximum power radiated and it is used for gain calculation. The total radiated power is calculated only if the NTF post-processing is active and it is obtained through the integration operation. There are two options for radiated power calculation, corresponding directly to the radiation pattern calculation regime:
Integration in the near-zone – it is the basic method to be used since it is fast and in most cases very accurate. In this option the radiated power is obtained by integrating the Poynting vector over the surface of the NTF box. This calculation procedure in invoked for a calculation of a single radiation pattern in a chosen Theta or Phi plane over the Phi or Theta angle respectively, and is signalised with active NTF fields option. This option is fast but may produce inaccurate results in two cases:
- NTF transformation in a lossy background medium, when power integrated over the NTF box depends on the box shape and size (see discussion below).
- NTF box positioned close to a radiating dipole and propagating fields on the box are mixed with the static mode (refer to User Guide V2D: Dipoles in air and dielectric media for example of such case).
Integration in the far zone – this option is general since the radiated power is obtained by integration along the 3D radiation pattern in the far zone. This calculation procedure is invoked with a calculation of Multiple radiation patterns (2D radiation patterns creating 3D pattern). However, this procedure (signalised with 3D patterns option) is very time-consuming because many 2D radiation patterns versus Phi and Theta must be calculated. Therefore it is recommended only for some special applications or as a way of testing the accuracy of the usually applied approach based on NTF fields.
It should be noted that in QW-V2D, this option is as fast as the first one, as the radiation characteristics are numerically calculated for one E- and H-plane, and analytically integrated in the Phi direction.
It is worth noting at this point that the value of Pr integrated over the NTF box is ambiguous and may be misleading in a lossy medium. Due to power density attenuation away from the source, this value depends not only on box size but also on its aspect ratios and placement with respect to the radiating structure. Thus the question is how to obtain the value of Pr for an antenna radiating into a lossy medium. There are three options, which are exemplified on User Guide 3D: Near-to-Far field transformation in non-air and lossy regions:
By integration over the 3D radiation patterns in the far zone. This option is rigorous and unambiguous; it produces radiated pattern scaled to the distance of 1 mm from the reference point, which may easily be scaled to any other distance via Pr~exp(-2a r) rule. Unfortunately, this procedure is very time-consuming, since many 2D characteristics must be calculated.
By integration of the Poynting vector over the NTF box. This option is fast and, although ambiguous as explained above, it will give a reasonable approximation (around few percent) in the case of relatively small NTF box and relatively small losses.
From the value of return loss and power available from the source. In QW-3D the scaling of excitation is such that pulse amplitude of 1 means 1 W time-maximum available power at the centre frequency for pulse duration tending to infinity. This means 1 W for sinusoidal waveform at its frequency and 1 W wide-band for a delta pulse. For band-limited pulses, power varies with frequency and spectrum depends on the pulse duration; only with the duration of tens of upper-frequency periods we approach 1 W reasonably flat within the band. The actual spectrum of the excitation pulse can be observed via Power Available post-processing.
It must be noted that the radiated power is positive when it is outgoing through the NTF box, which is the case in typical antenna simulations. In the analysis of scattering problems (when one wants to also monitor the power incoming from the plane wave box and the NTF box is placed inside the PLW box), net power may be incoming through the NTF box, in which case the value of Pr is negative.
The value of Pr is available in the status bar of the 2D radiation pattern Results window if only one NTF frequency is considered. If more NTF frequencies are analysed, Antenna Parameters column contains this value for each frequency.
In case of antennas, the influence of losses on circuit performance is quantitatively described by radiation efficiency (Ef). The antenna radiation efficiency is calculated for NTF post‑processing and is defined as the ratio of the radiated power (Pr) to the power injected into the antenna by the source (Pi):
Ef = Pr / Pi
The value of Ef at a given NTF frequency is calculated only if the S-Parameters post-processing at a source are active and one of its frequencies coincides with the NTF frequency. Only with the S-Parameters post-processing active the software has enough information to calculate the actual power injected by the source. If those conditions are not obeyed, Ef=0 is displayed.
Note that in the case of multi-port antennas, the value of Pi, and consequently Ef, change as one includes or excludes certain ports in S-Parameters post-processing. For example, in the case of a waveguide slot antenna, if both waveguide input and output are included in the S‑Parameters post-processing, the slot radiation efficiency is calculated with respect to the net power (difference between power injected by the waveguide source and power that exits via the waveguide load). If only the source is included in the S-Parameters post-processing, the slot radiation efficiency is calculated with respect to the power injected by the waveguide source and as a consequence, will be lower than in the first case.
Note that in the case of lossless structures, and all ports included in the S-Parameters post‑processing, the value of efficiency can be used as a quantitative measure of convergence of the simulation: efficiency of 100% means that all the delivered power has left the computational volume, and thus the results will not change.
The value of Ef is available in the status bar of the 2D radiation pattern Results window if only one NTF frequency is considered. If more NTF frequencies are analysed, Antenna Parameters column contains this value for each frequency.
QuickWave delivers a value of antenna radiation resistance (Rr) at a given NTF frequency. Radiation resistance is defined as a ratio of radiated power (Pr) to the square of amplitude of current injected into the antenna by a point source:
Rr = Pr / |I|2
This entails that two types of post-processing: NTF and FD-Probing must be active in order to find antenna radiation resistance. If there is no point source feeding antenna, the amplitude of the current injected into the antenna and as a consequence the antenna radiation resistance will not be calculated and the displayed value of Rr will be 0.
The value of Rr is calculated only if the FD-Probing post-processing at a lumped source is active and one of its frequencies coincides with the given NTF frequency; otherwise Rr=0 is displayed.
The value of Rr is available in the status bar of the 2D radiation pattern Results window if only one NTF frequency is considered. If more NTF frequencies are analysed, Antenna Parameters column contains this value for each frequency.
6.2.9.9 Power injected by source
QuickWavedelivers a value of the time-maximum power injected into antenna by the source (Pi) at a given NTF frequency. The way of calculating the power injected by the source is explained earlier of this manual, where this power is denoted as power delivered by the source PD. The value of Piis calculated only if the S-Parameters post-processing at a source is active and one of its frequencies coincides with the given NTF frequency. Only with the S‑Parameters post-processing active the software has enough information to calculate the actual power injected by the source. If those conditions are not obeyed Pi=0 is displayed.
Note that in the case of multi-port antennas, the value of Pi changes as one includes or excludes certain ports in S-Parameters post-processing. For example, in the case of a waveguide slot antenna, if both waveguide input and output are included in the S‑Parameters post-processing, the Pi will be the net power that is a difference between power injected by the waveguide source and power that exits via the waveguide load. If only the source is included in the S-Parameters post-processing, the Pi equals to the power injected by the waveguide source and will be higher than in the first case.
The value of Pi is available in the Antenna Parameters column of the 2D radiation pattern Results window. If its value is close to zero this means that calculations of antenna efficiency may be ill-conditioned.
6.2.9.10 Current injected by source
QuickWavedelivers a value of square of the amplitude of current injected into the antenna by a point source (|I|^2) at a given NTF frequency. The value of |I|^2 is calculated only if the FD-Probing post-processing at a point source is active and one of its frequencies coincides with the given NTF frequency; otherwise |I|^2=0 is displayed. If there is no lumped source feeding antenna, the amplitude of the current injected into the antenna will not be calculated and its value will be 0.
The value of |I|^2 is available in the Antenna Parameters column of the 2D radiation pattern Results window.
QuickWave extracts the radiation patterns in linear polarisation. Polarisation definition is based on the direction of the E-field with respect to the angular components Phi and Theta, thus for the linear polarisation, Etheta and Ephi curves are extracted.
In QW-V2D, for linear polarisation such results as Copl (co- polarisation) and Cxpl (cross‑polarisation) are additionally available. Those characteristics are calculated according to the definition given in "Foundations of antennas. A unified approach" by Per-Simon Kildal and were introduced in QW-V2D to allow the user retrieving the information about circular polarisation (using Ludwig's definitions).
6.2.9.12 Circular Polarisation
Except for extracting radiation patterns in linear polarisation (Etheta and Ephi curves), it is also possible to switch to circular polarisation (Eleft and Eright curves). The convention for the left-handed Eleft and right-handed Eright circular polarisation is that for the outgoing wave.
If the analysed antenna is linearly polarised (one of Etheta or Ephi components is obviously dominant and the other is zero), the left- and right-handed polarisation curves practically overlap.
If the Etheta and Ephi curves are equal in magnitude and phase-shifted by 90 degrees, upon switching to circular polarisation circularly polarised wave will be observed with Eleft or Eright component being dominant. For more discussion please refer to User Guide 3D: Radiation patterns for circular polarisation example.
QuickWave calculates the Axial Ratio curves for antenna analysis. Axial ratio delivers information about the polarisation of the antenna since it is calculated from the ratio of the polarisation ellipse’s axes. If Axial Ratio=1 the antenna polarisation is circular. If the antenna is linearly polarised, the Axial Ratio will be equal to 0. The Axial Ratio curves are calculated for the Circular Polarisation option of the 2D radiation pattern Results window.
6.2.9.14 Far field 3D radiation pattern
In some cases, the user may wish to see a 3D radiation pattern, with both Theta and Phi angles varying in steps. Such option is enabled in QW-Simulator in 3D Radiation Pattern window. It must be noted at this point that these calculations may be quite time consuming.
The far field pattern is calculated in a spherical coordinate system with one Reference Axis (X, Y or Z) and two angles: elevation (Theta) and azimuthal (Phi). A fine Step for Theta and Phi angles leads to smooth 3D pattern but costs longer time for its construction. Note that step reduction for both angles by a factor of two increases the construction time by a factor of 4. The 3D radiation pattern is available for all NTF frequencies set for the NTF post-processing in the Input Interface. The 3D patterns may be constructed to show magnitudes of:
only Etheta
only Ephi
a vectorial sum of both Etheta and Ephi components
only Eleft
only Eright
a vectorial sum of both Eleft and Eright components.